3 Modelagem com dados reais

Muitos dados, gaussianos ou não, podem ser modelados através dos métodos apresentados na seção 2. Nessa seção vamos considerar a temperatura média anual, em graus Fahrenheit, do Central Park, em Nova Iorque. Todas as análises feitas nessa seção foram feitas com a utilização do software R R Core Team (2020) e do pacote forecast (Hyndman et al. (2020); Hyndman and Khandakar (2008)).

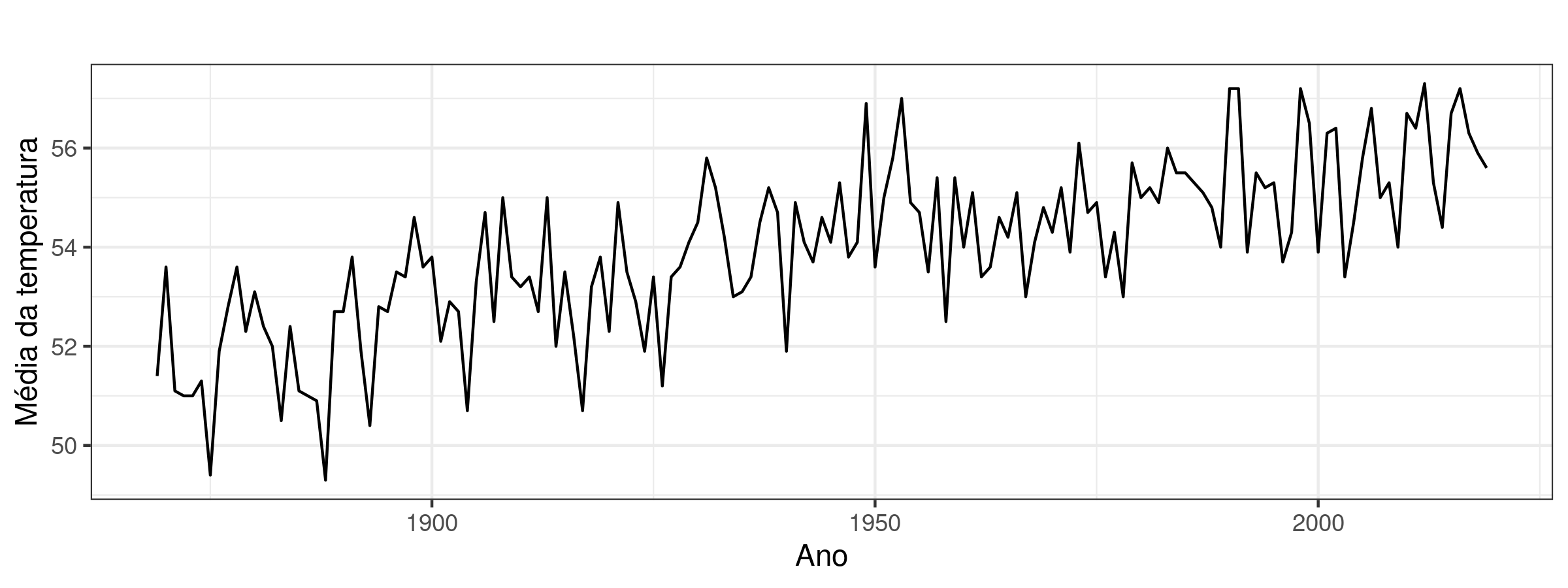
Série temporal da temperatura média anual (em graus Fahrenheit) no Central Park dos anos de 1869 até 2019.

Figura 3.1: Série temporal da temperatura média anual (em graus Fahrenheit) no Central Park dos anos de 1869 até 2019.

A base de dados contém as temperaturas médias anuais de 1869 até 2019, totalizando 151 observações. A Figura 3.1 mostra a tempertura média ao longo dos anos. A Figura 3.2 mostra a série diferenciada uma vez. Para checar a hipótese de estacionaridade, realizamos um teste de Kwiatkowski–Phillips–Schmidt–Shin (KPSS) Kwiatkowski et al. (1992). Com 99% de confiança, o teste mostrou que a série não é estacionária e passa a ser estacionária logo na primeira diferenciação, como pode ser visto no Código 3.1. A autocorrelação dos dados e da primeira diferença estão na Figura 3.3.

Código 3.1 Teste KPSS 
## Lê o conjunto de dados
dd <- data.table::fread("monthly.csv")
## Converte para ts
serie <- ts(dd$ANNUAL[-152], start = 1869, end = 2019)

## Os dados são estacionários?
summary(urca::ur.kpss(serie))
## 
## ####################### 
## # KPSS Unit Root Test # 
## ####################### 
## 
## Test is of type: mu with 4 lags. 
## 
## Value of test-statistic is: 2.5848 
## 
## Critical value for a significance level of: 
##                 10pct  5pct 2.5pct  1pct
## critical values 0.347 0.463  0.574 0.739
summary(urca::ur.kpss(diff(serie)))
## 
## ####################### 
## # KPSS Unit Root Test # 
## ####################### 
## 
## Test is of type: mu with 4 lags. 
## 
## Value of test-statistic is: 0.0179 
## 
## Critical value for a significance level of: 
##                 10pct  5pct 2.5pct  1pct
## critical values 0.347 0.463  0.574 0.739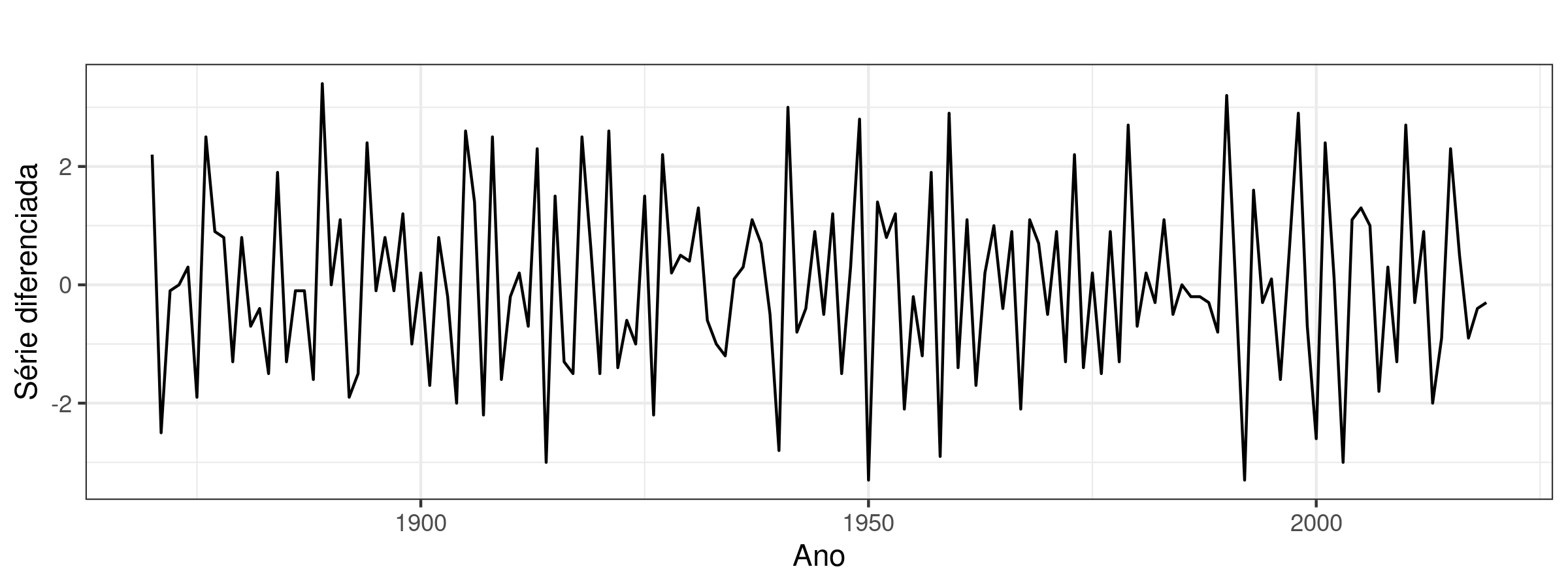
Série temporal da temperatura média anual (em graus Fahrenheit) no Central Park dos anos de 1869 até 2019 com um nível de defasagem.

Figura 3.2: Série temporal da temperatura média anual (em graus Fahrenheit) no Central Park dos anos de 1869 até 2019 com um nível de defasagem.

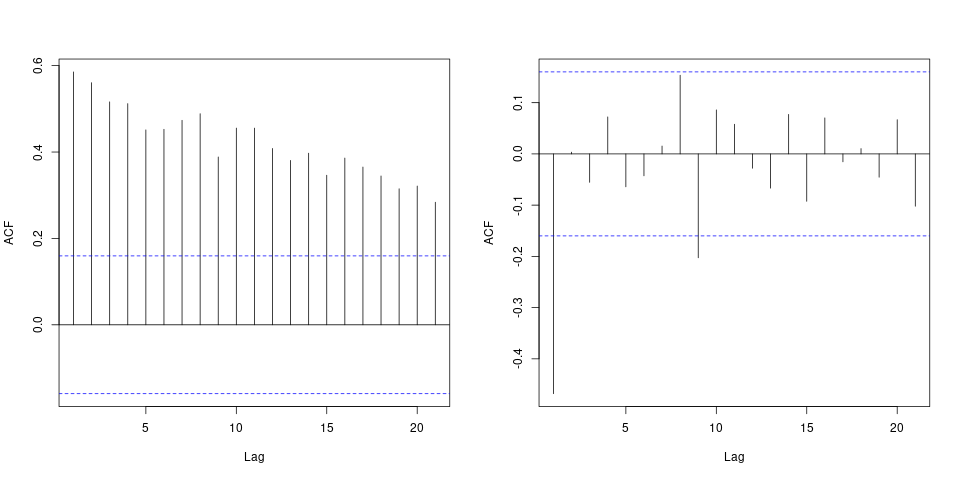
Diferentes valores de defasagem de autocorrelação da série original (esq.) e para a primeira diferença da série histórica (dir.).

Figura 3.3: Diferentes valores de defasagem de autocorrelação da série original (esq.) e para a primeira diferença da série histórica (dir.).

Tabela 3.1: Diferentes valores de AIC e parâmetros estimados para cada modelo ARIMA.
Modelo AIC ĉ θ̂ ϕ̂
ARIMA(0,0,0) 590.84 53.97
ARIMA(0,0,1) 556.85 53.96 0.39
ARIMA(0,1,0) 553.88
ARIMA(1,0,0) 528.15 53.96 0.59
ARIMA(0,1,1) 481.78 -0.86
ARIMA(1,0,1) 489.63 53.87 -0.85 0.99
ARIMA(1,1,0) 518.51 -0.47
ARIMA(1,1,1) 483.28 -0.87 0.06

A Tabela 3.1 mostra o AIC e os parâmetros estimados de cada modelo ajustado por máxima verossimilhança aos dados. O modelo que melhor se ajustou foi ARIMA(0, 1, 1), com \(\hat{\sigma}^2\) = 1.4 e \(\hat{Var}(\hat{\theta}) = 0.0016\). Portanto, a equação do modelo ajustado é dada por:

\[\begin{equation*} \hat{Y}'_t = -0.8561 (\hat{Y}_{t-1} - Y_{t-1}) \hspace{0.3cm} \text{com } t = 2, 3, \ldots, 151. \end{equation*}\]

A Figura 3.4 mostra os resíduos do modelo ajustado. O resíduo apresenta padrão aleatório e não há valores extremos, indicando que não temos problemas com falta de ajuste, também, notamos que não há relação entre média e variância. A Figura 3.5 mostra que não temos problemas de resíduos autocorrelacionados. Os resíduos também se aderem à distribuição Normal, porém com caudas mais leves, como pode ser visto na Figura 3.6.

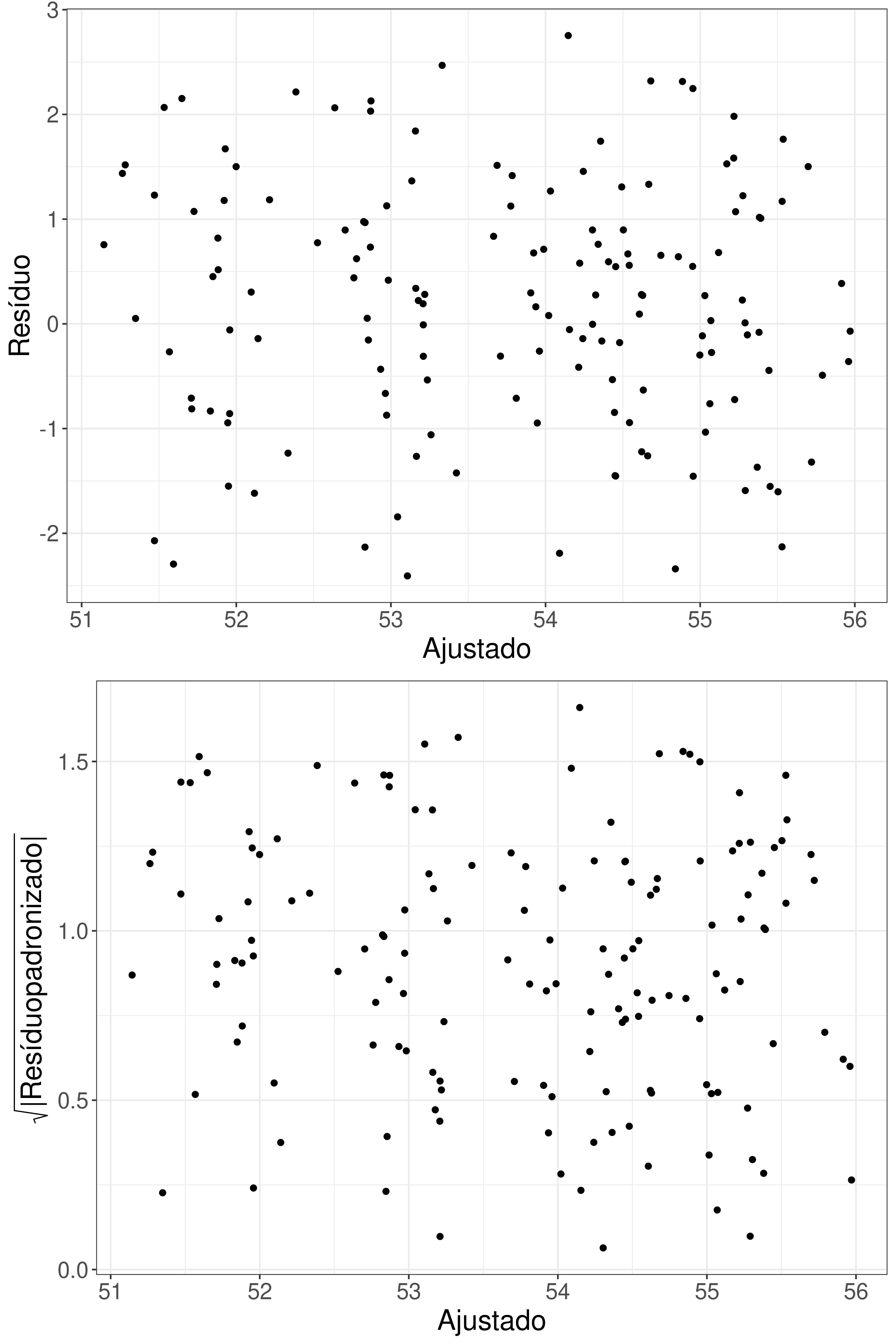
Resíduos (acima) e raíz quadrada do valor absoluto dos resíduos padronizados para cada valor ajustado pelo modelo ARIMA(0,1,1).

Figura 3.4: Resíduos (acima) e raíz quadrada do valor absoluto dos resíduos padronizados para cada valor ajustado pelo modelo ARIMA(0,1,1).

Autocorrelação dos resíduos para diferentes valores de defasagem ajustados pelo modelo ARIMA(0,1,1).

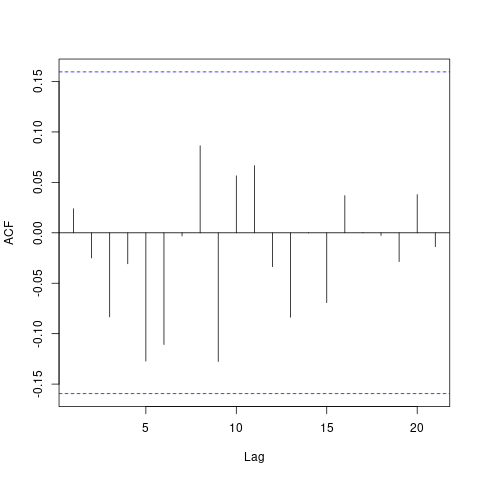
Figura 3.5: Autocorrelação dos resíduos para diferentes valores de defasagem ajustados pelo modelo ARIMA(0,1,1).

Gráfico quantil-quantil dos resíduos ajustados pelo modelo ARIMA(0,1,1).

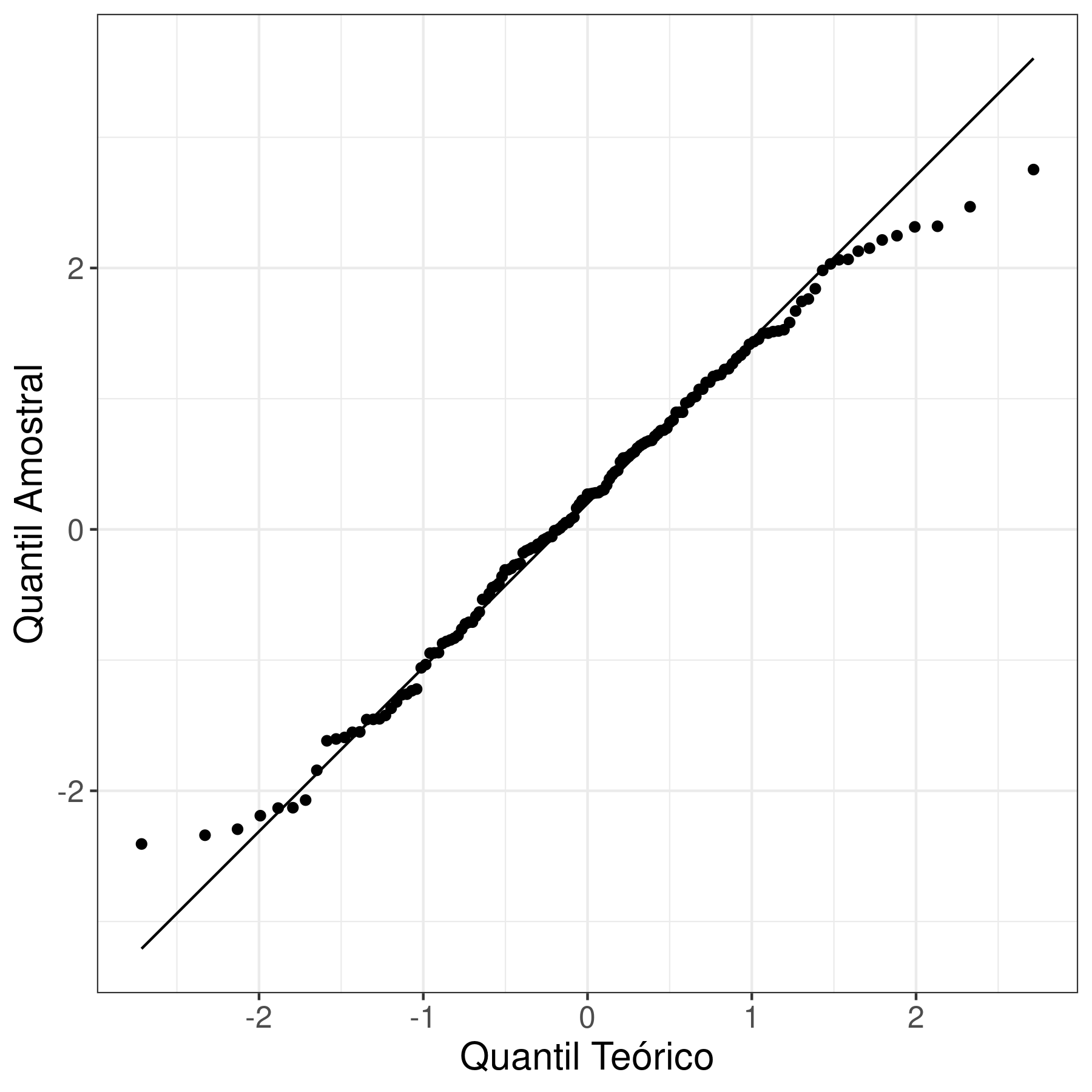
Figura 3.6: Gráfico quantil-quantil dos resíduos ajustados pelo modelo ARIMA(0,1,1).

Para finalizar, a Figura 3.7 mostra a série com o intervalo com 95% de confiança para cada valor ajustado e um intervalo de predição com 95% de confiança para os anos de 2020 a 2024. Como o modelo ajustado desconsiderou os valores da parte auto-regressiva, a estimativa pontual é constante para a predição.

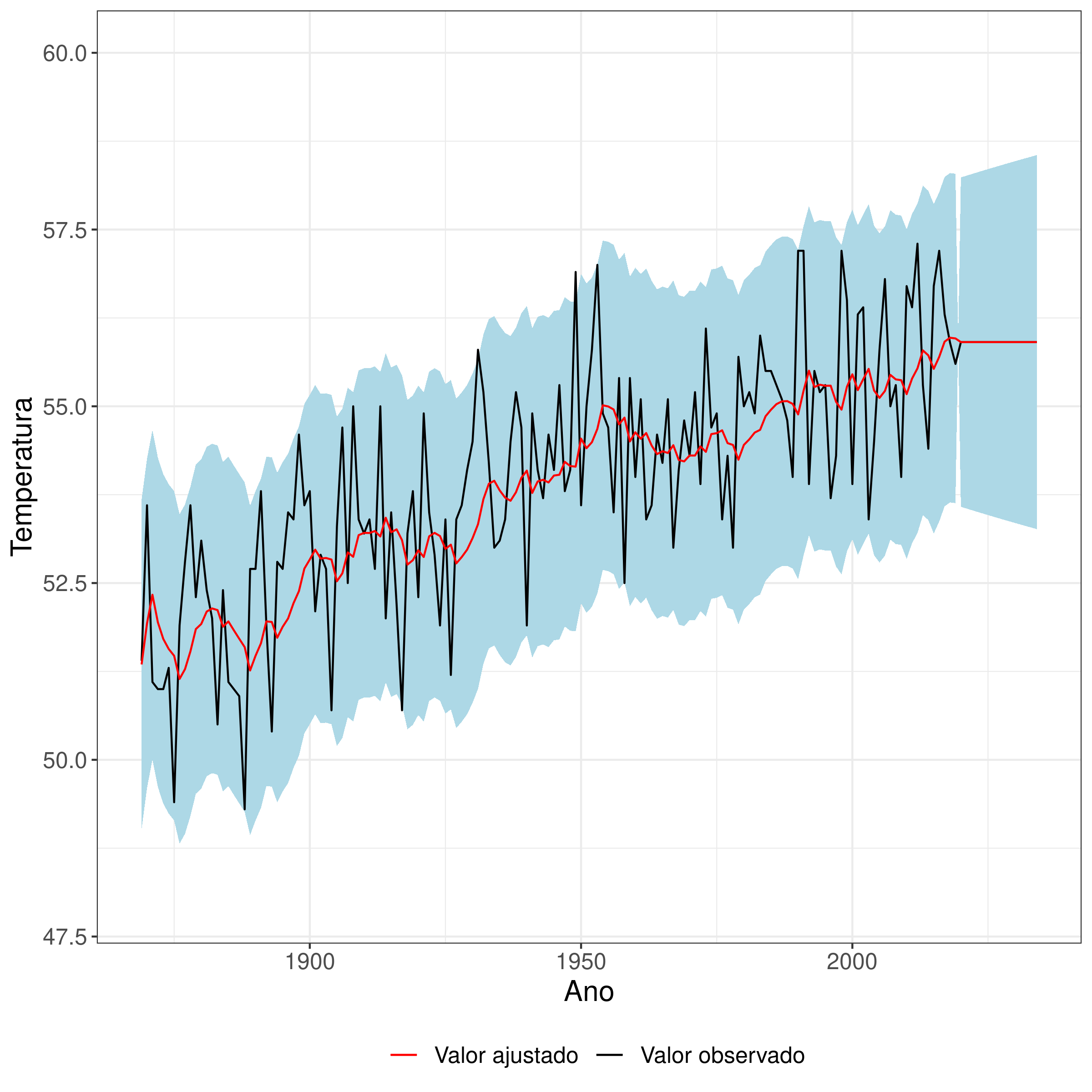
Gráfico da temperatura média anual (em graus Fahrenheit) do Central Park observada (preto) e ajustada (vermelho) pelo modelo ARIMA(0,1,1). Em azul está o intervalo de confiança e o intervalo de predição de 2020 até 2024 (ambos com 95\% de confiança).

Figura 3.7: Gráfico da temperatura média anual (em graus Fahrenheit) do Central Park observada (preto) e ajustada (vermelho) pelo modelo ARIMA(0,1,1). Em azul está o intervalo de confiança e o intervalo de predição de 2020 até 2024 (ambos com 95% de confiança).