3 Resultados e dicussão
3.1 Análise descritiva
A Figura 3.1 mostra um gráfico de pontos das variáveis da
base versus as outras com uma reta ajustada via regressão linear simples, um
gráfico de barras (ou histograma, para as variáveis contínuas) e o coeficiente
de correlação produto-momento das variáveis. A base de dados contém 514 anúncios
de processadores de computadores de mesa das marcas AMD e Intel. Há
processadores com data de lançamento de 2005 até 2020. Na base há 205
observações de processadores AMD e 309 de processadores Intel. O preço está em
R$ e a frequência máxima de processamento está em GHz. A variável
preco_transformado é variável resposta após uma transformação raíz
quinta. Nessa escala, os dados têm melhor comportamento do que na escala
original, a correlação entre as variáveis teve uma melhoria e a variabilidade é
menor. Encontramos esse valor através de método de Box-Cox (Box and Cox (1964)).
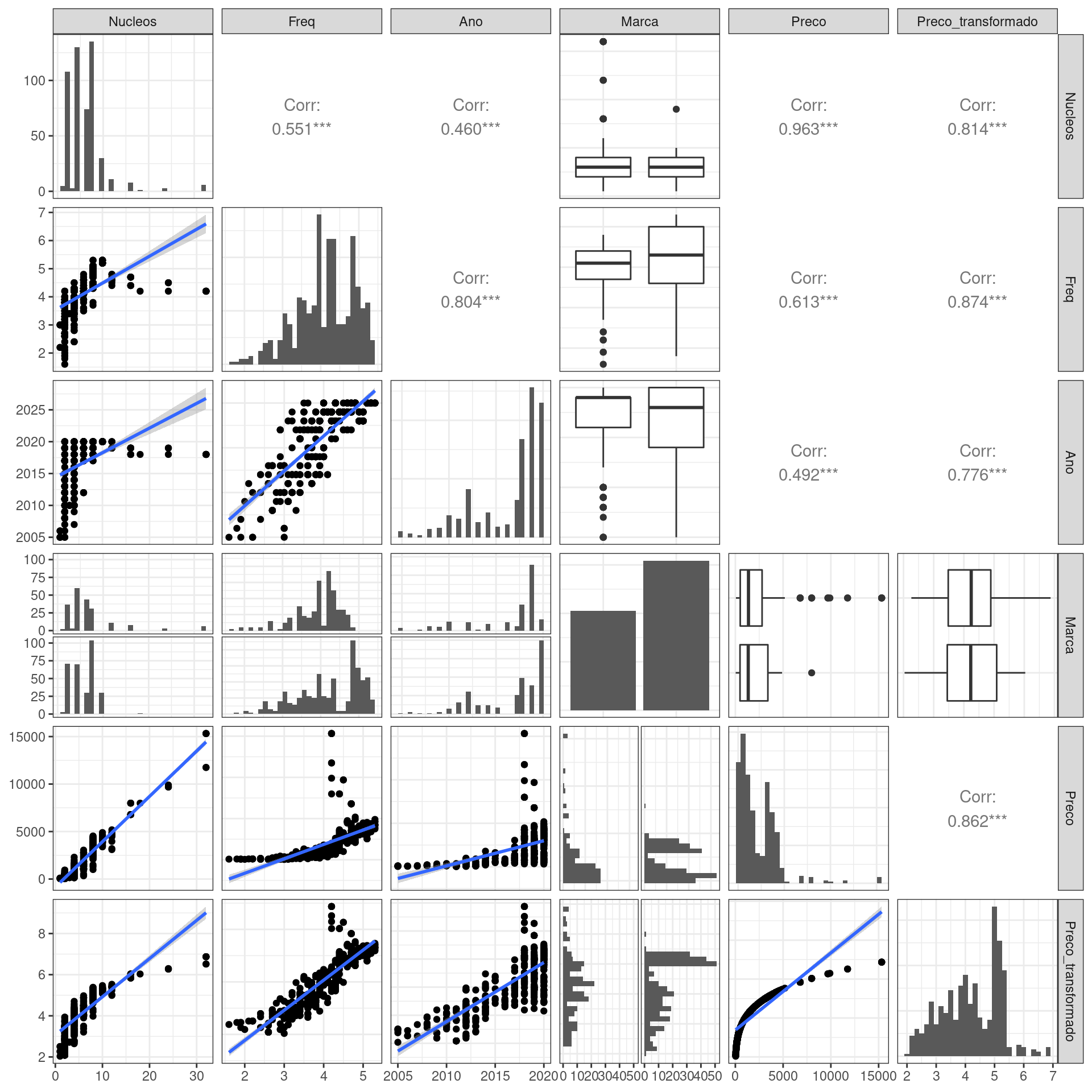
Figura 3.1: Análise descritiva do conjunto de dados com uma reta ajustada via regressão linear simples entre as variáveis e o coeficiente de correlação de Pearson.
Podemos ver que as covariáveis são correlacionadas linearmente entre si e correlacionadas com a variável resposta, essas correlações sempre positivas.
Para o ajuste do modelo, vamos utilizar o preço transformado. Também, notamos que uma reta não é suficiente para explicar a relação entre a variável resposta e as demais covariáveis.
A variável resposta é assimétrica em ambas escalas, porém com a transformação isso reduziu. Percebemos que há poucos anúncios de processadores com mais de 10 núcleos e de processadores mais antigos. Ainda, não parece haver diferença média significativa entre as marcas.
3.2 Ajuste do modelo
Após testar diversos modelos, o que melhor se ajustou aos dados foi:
\[ E(Y_i | \mathbf{x}_i^t) = \hat{\beta_0} + \hat{\beta_1}x_{ifreq} + \hat{\beta_2} x_{ifreq}^2 + \hat{\beta_3} x_{ifreq}^3 + \hat{\beta_4}x_{iano} + \hat{\beta_5} x_{iano}^2 + \hat{\beta_6} x_{iano}^3 + \hat{\beta_7} x_{inucleos} + \hat{\beta_8} x_{inucleos}^2 \]
No anexo do projeto encontra-se uma tabela comparando a critérios de qualidade de ajuste para diversos modelos ajustados aos dados.
Ajustamos os modelos no software R (R Core Team (2021)). Utlizamos a função poly para
encontrar polinômios ortogonais para as variáveis. A desvantagem de sua
utilização é que a interpretação dos valores ajustados não é simples.
O ajuste e resumo do modelo ajustado estão no Código 3.1:
dt <- data.table::fread("../dados/processadores.csv", sep = ";")
## Ajusta o modelo
fit <- lm(Preco^0.2 ~ poly(Freq, 3) + poly(Nucleos, 2) + poly(Ano, 3), data = dt)
## Resumo do ajuste
summary(fit)##
## Call:
## lm(formula = Preco^0.2 ~ poly(Freq, 3) + poly(Nucleos, 2) + poly(Ano,
## 3), data = dt)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.73608 -0.11750 -0.00553 0.12822 0.66145
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.192944 0.009105 460.510 < 2e-16 ***
## poly(Freq, 3)1 9.107335 0.472834 19.261 < 2e-16 ***
## poly(Freq, 3)2 0.639123 0.266753 2.396 0.01694 *
## poly(Freq, 3)3 -0.803299 0.244029 -3.292 0.00107 **
## poly(Nucleos, 2)1 11.433445 0.302089 37.848 < 2e-16 ***
## poly(Nucleos, 2)2 -2.599557 0.321110 -8.096 4.29e-15 ***
## poly(Ano, 3)1 3.700255 0.377977 9.790 < 2e-16 ***
## poly(Ano, 3)2 -0.828141 0.253659 -3.265 0.00117 **
## poly(Ano, 3)3 -2.512418 0.227228 -11.057 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2064 on 505 degrees of freedom
## Multiple R-squared: 0.9577, Adjusted R-squared: 0.9571
## F-statistic: 1430 on 8 and 505 DF, p-value: < 2.2e-16## Tabela ANOVA
anova(fit)## Analysis of Variance Table
##
## Response: Preco^0.2
## Df Sum Sq Mean Sq F value Pr(>F)
## poly(Freq, 3) 3 402.93 134.311 3152.005 < 2.2e-16 ***
## poly(Nucleos, 2) 2 74.50 37.251 874.213 < 2.2e-16 ***
## poly(Ano, 3) 3 10.02 3.341 78.407 < 2.2e-16 ***
## Residuals 505 21.52 0.043
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Os resultados mostram que o modelo teve um bom ajuste. A quantidade explicada pela regressão (\(R^2\)) mostra que o modelo explicou bem a variação dos preços. Nota-se que o \(R^2\) ajustado (o que penaliza por número de parâmetros) ficou próximo ao valor não penalizado.
Pelos valores do fator de inflação de variância generalizado, não há indício de multicolinearidade no ajuste.
car::vif(fit)## GVIF Df GVIF^(1/(2*Df))
## poly(Freq, 3) 11.366183 3 1.499463
## poly(Nucleos, 2) 3.616474 2 1.379022
## poly(Ano, 3) 6.085672 3 1.351195O modelo declarado não apresenta falta de ajuste, como pode ser visto nas Figuras 3.2 e 3.3. A Figura 3.3 mostra que a relação do tipo média-variância não está ideal. Também, os resíduos se adequaram bem à distribuição Normal, com fuga de alguns pontos nas caudas. A Figura 3.4 mostra que há pontos com alta alavancagem e influentes. As observações influentes não devem ser retiradas, uma vez que seus registros foram verificados e elas fazem parte da população de interesse. Além disso, há poucos poucas observações nos maiores valores do domínio do preço, como foi visto na análise descritiva dos dados. Nessa área, os resíduos parecem ter uma variância diferente dos anteriores.
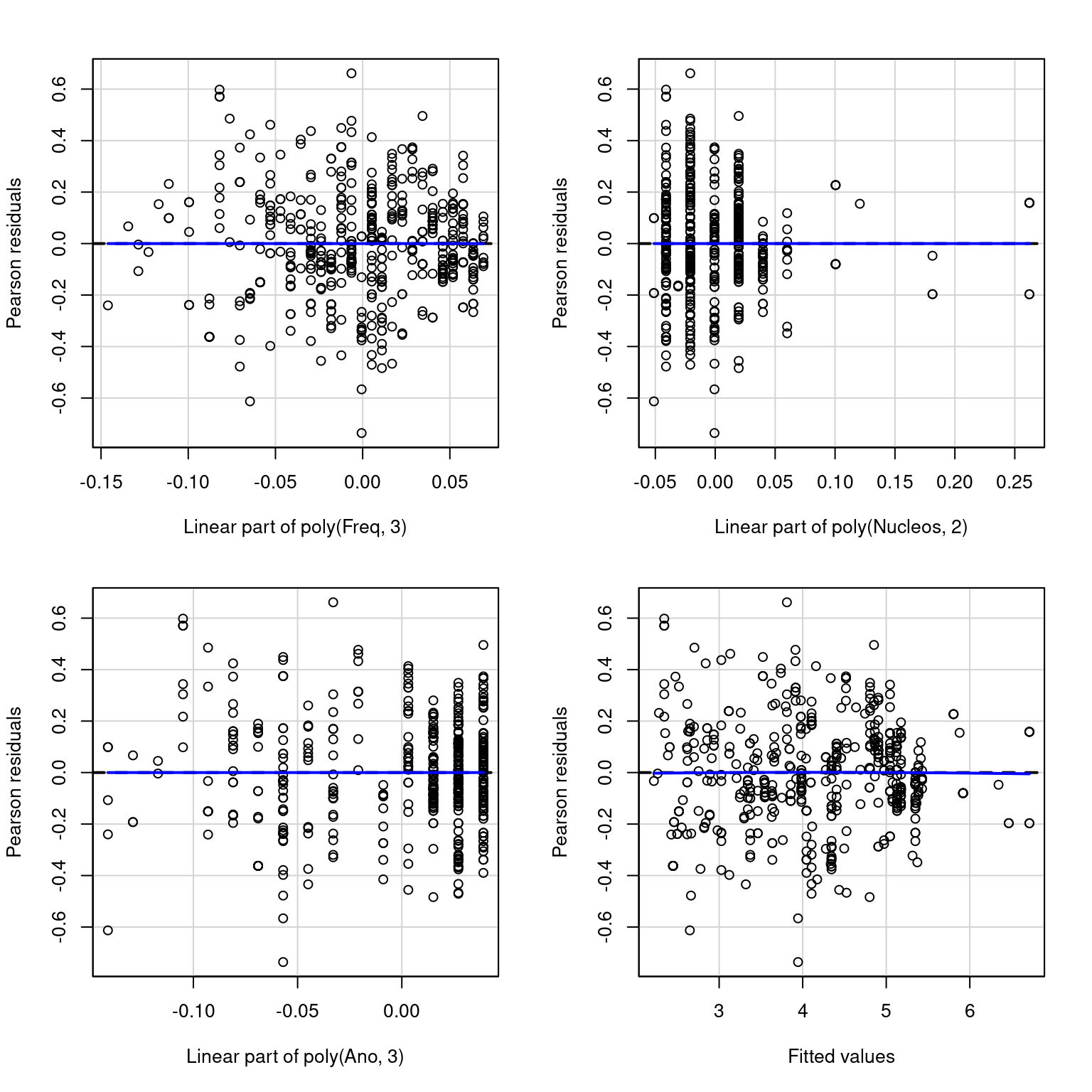
Figura 3.2: Análise de diagnóstico do primeiro modelo ajustado. Resíduos versus cada termo de maior ordem do modelo.
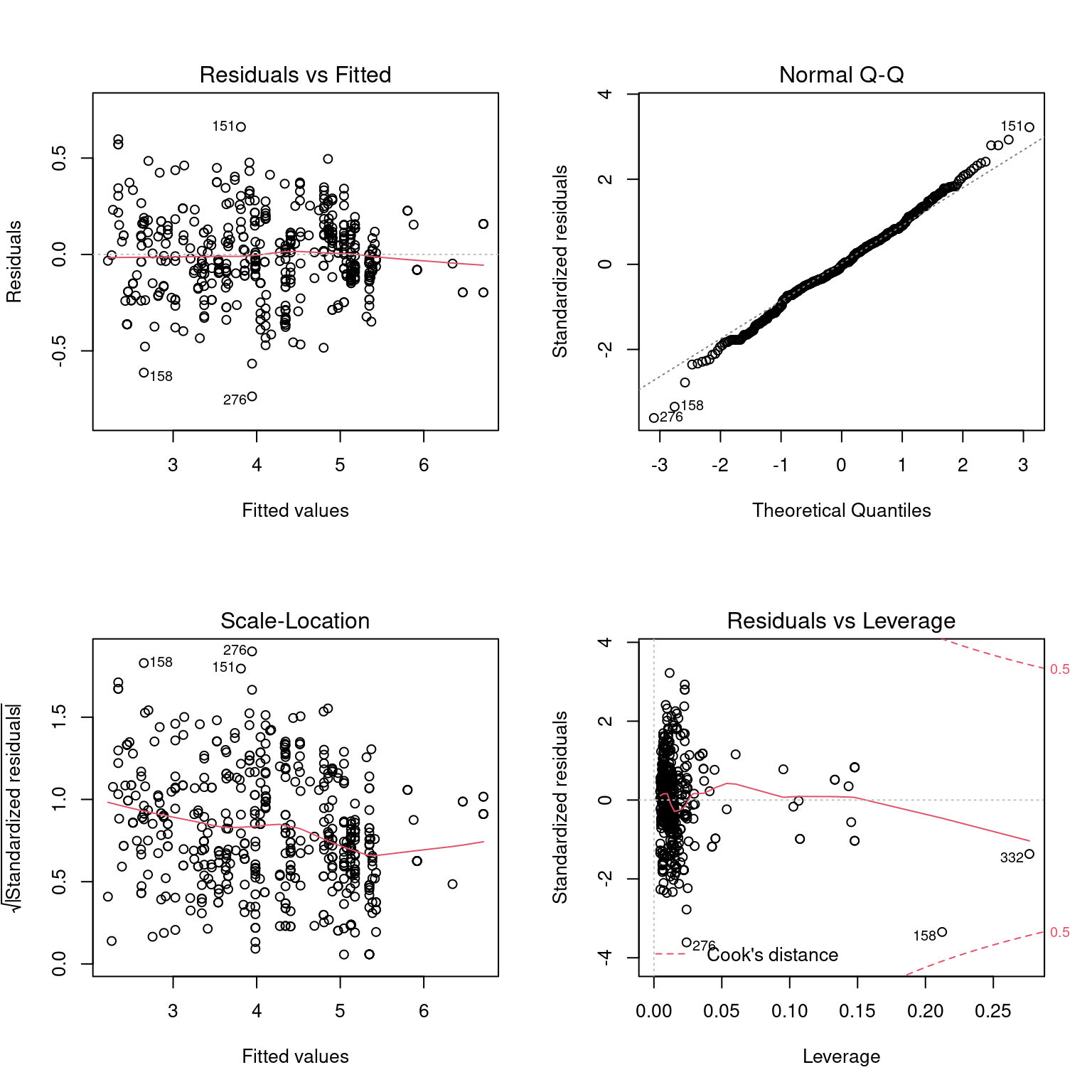
Figura 3.3: Análise de diagnóstico do primeiro modelo ajustado. Resíduos versus valores ajustado (superior esquerda), raíz quadrada do valor absoluto dos resíduos padronizados (inferior esquerda), gráfico quantil-quantil dos resíduos (superior direita) e resíduos padronizados versus alavancagem (inferior direita).
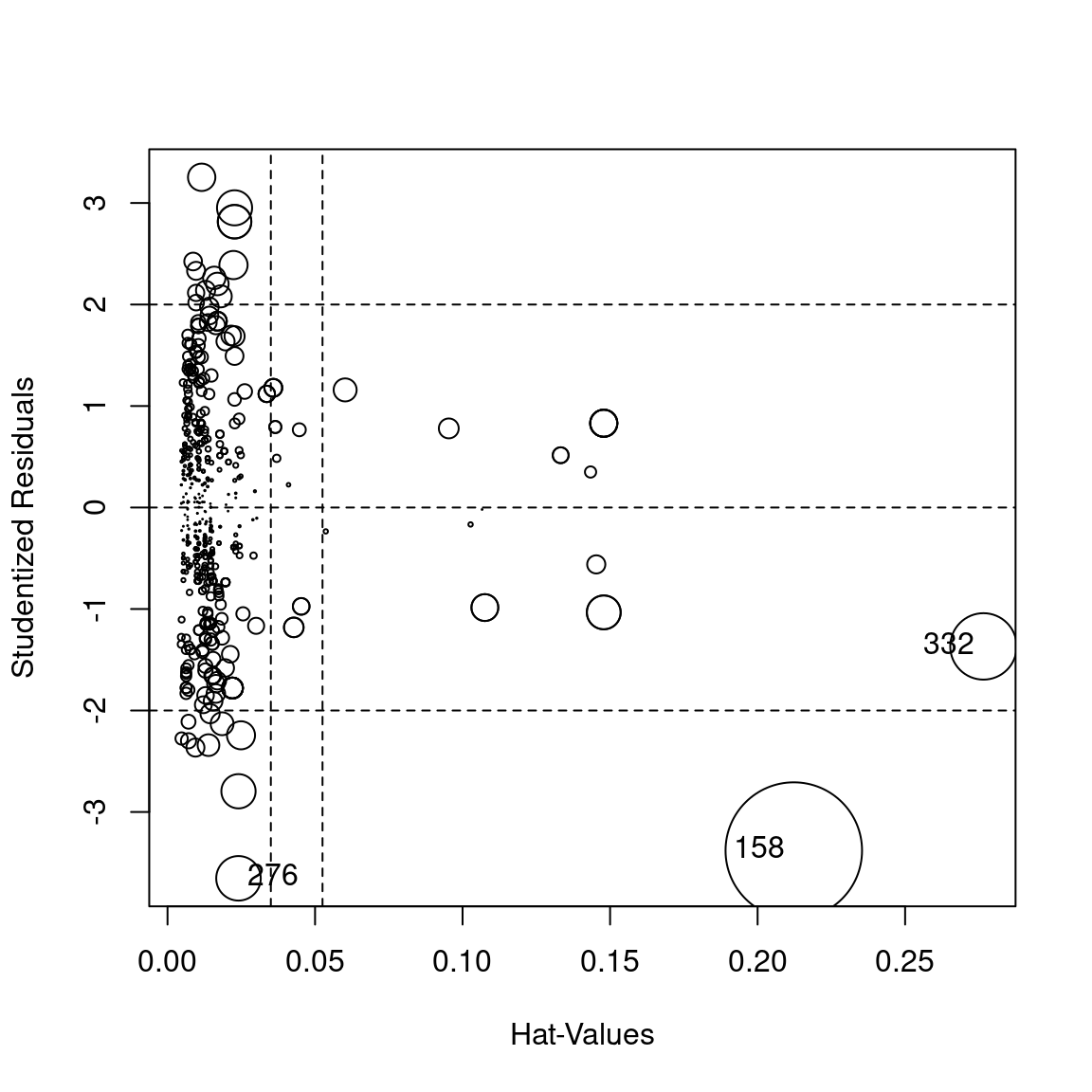
Figura 3.4: Análise de diagnóstico do primeiro modelo ajustado. Gráfico de influência dos resíduos. Quanto maior for o círculo, maior é a distância de Cook.
## StudRes Hat CookD
## 158 -3.380072 0.21226754 0.33515083
## 276 -3.653400 0.02404898 0.03567219
## 332 -1.368472 0.27655660 0.07940705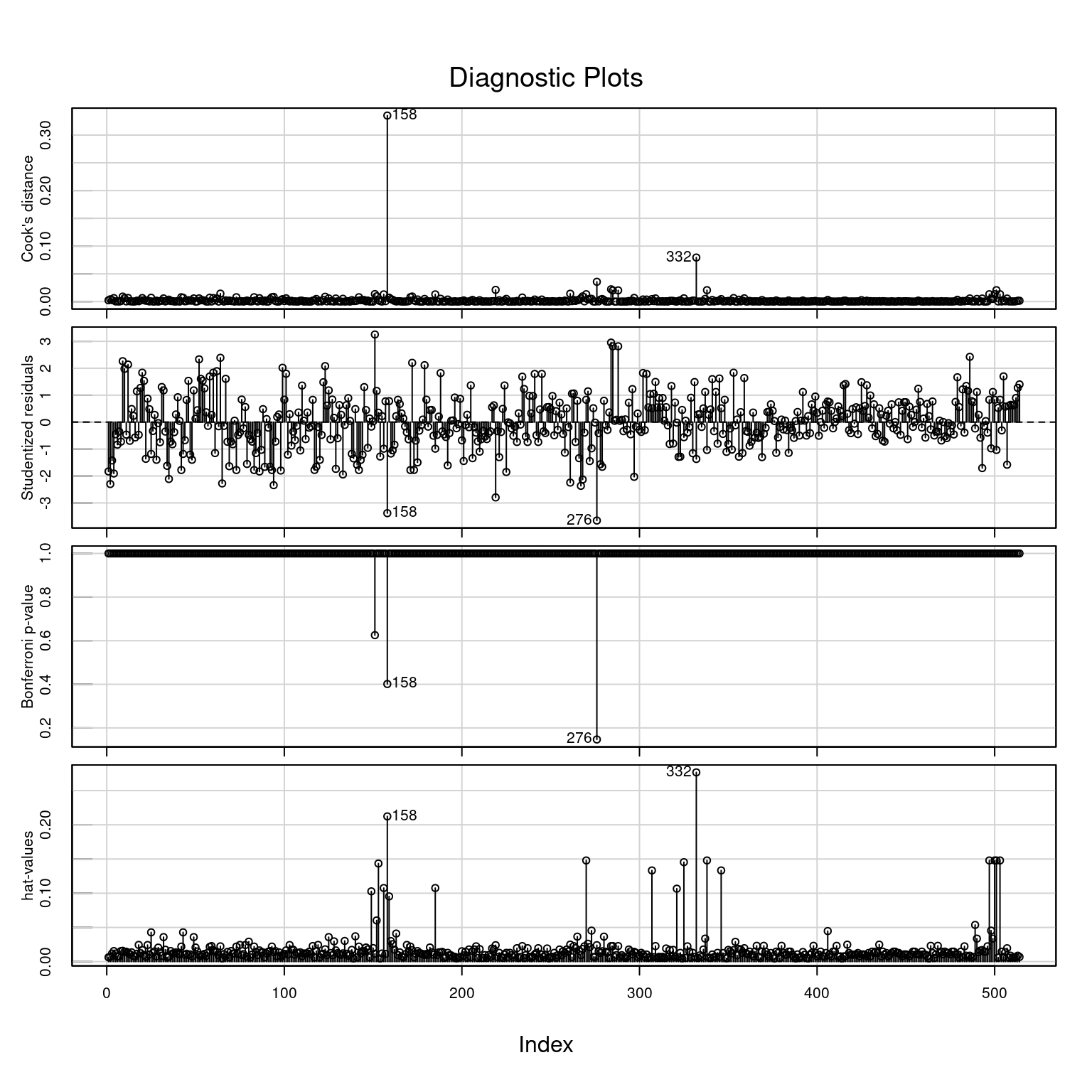
Figura 3.5: Análise de diagnósico do primeiro modelo ajustado. Outras medidas de influência para cada resíduo.
3.2.1 Medidas corretivas
Para lidar com os pontos influentes, ajustamos uma regressão robusta com \(\psi_{Biweight}\). Fixando a constante dessa regressão em \(k = 4.685\) para 95% de eficiência. Esse ajuste é feito no Código 3.2.
## Ajusta o modelo
fit2 <- MASS::rlm(Preco^0.2 ~ poly(Freq, 3) + poly(Nucleos, 2) + poly(Ano, 3),
data = dt, psi = MASS::psi.bisquare)Resumo do modelo:
summary(fit2)##
## Call: rlm(formula = Preco^0.2 ~ poly(Freq, 3) + poly(Nucleos, 2) +
## poly(Ano, 3), data = dt, psi = MASS::psi.bisquare)
## Residuals:
## Min 1Q Median 3Q Max
## -0.733963 -0.120638 -0.004154 0.129846 0.660298
##
## Coefficients:
## Value Std. Error t value
## (Intercept) 4.1922 0.0092 456.9444
## poly(Freq, 3)1 9.1225 0.4764 19.1475
## poly(Freq, 3)2 0.5298 0.2688 1.9710
## poly(Freq, 3)3 -0.8512 0.2459 -3.4616
## poly(Nucleos, 2)1 11.4633 0.3044 37.6599
## poly(Nucleos, 2)2 -2.6577 0.3236 -8.2140
## poly(Ano, 3)1 3.7151 0.3809 9.7545
## poly(Ano, 3)2 -0.7895 0.2556 -3.0887
## poly(Ano, 3)3 -2.6392 0.2290 -11.5271
##
## Residual standard error: 0.1799 on 505 degrees of freedomanova(fit2)## Analysis of Variance Table
##
## Response: Preco^0.2
## Df Sum Sq Mean Sq F value Pr(>F)
## poly(Freq, 3) 3 359.95 119.982
## poly(Nucleos, 2) 2 67.46 33.732
## poly(Ano, 3) 3 9.11 3.037
## Residuals 21.56Houve uma ligeira mudança nos valores dos parâmetros estimados, não iremos remover o coeficiente não significativo para (\(\alpha = 0.05\)) pelo princípio da hierarquia.
O diagnóstico dessa correção está na Figura 3.6. Com essa modificação, ainda constatamos um leve decaímento da variância com o aumento da média do preço. Os resíduos ainda aparentam ter distribuição Normal, com algumas fugas nas caudas. Ainda há pontos com influentes com alavancagem alta, porem em menor escala que o ajuste anterior. Também, notamos que com a modificação alguns pontos têm resíduos padronizados maiores que os anteriores, e até mesmo alguns candidatos a outlier. Não há razão para removê-los, uma vez que as observações são da população e não apresentam erro de registro.
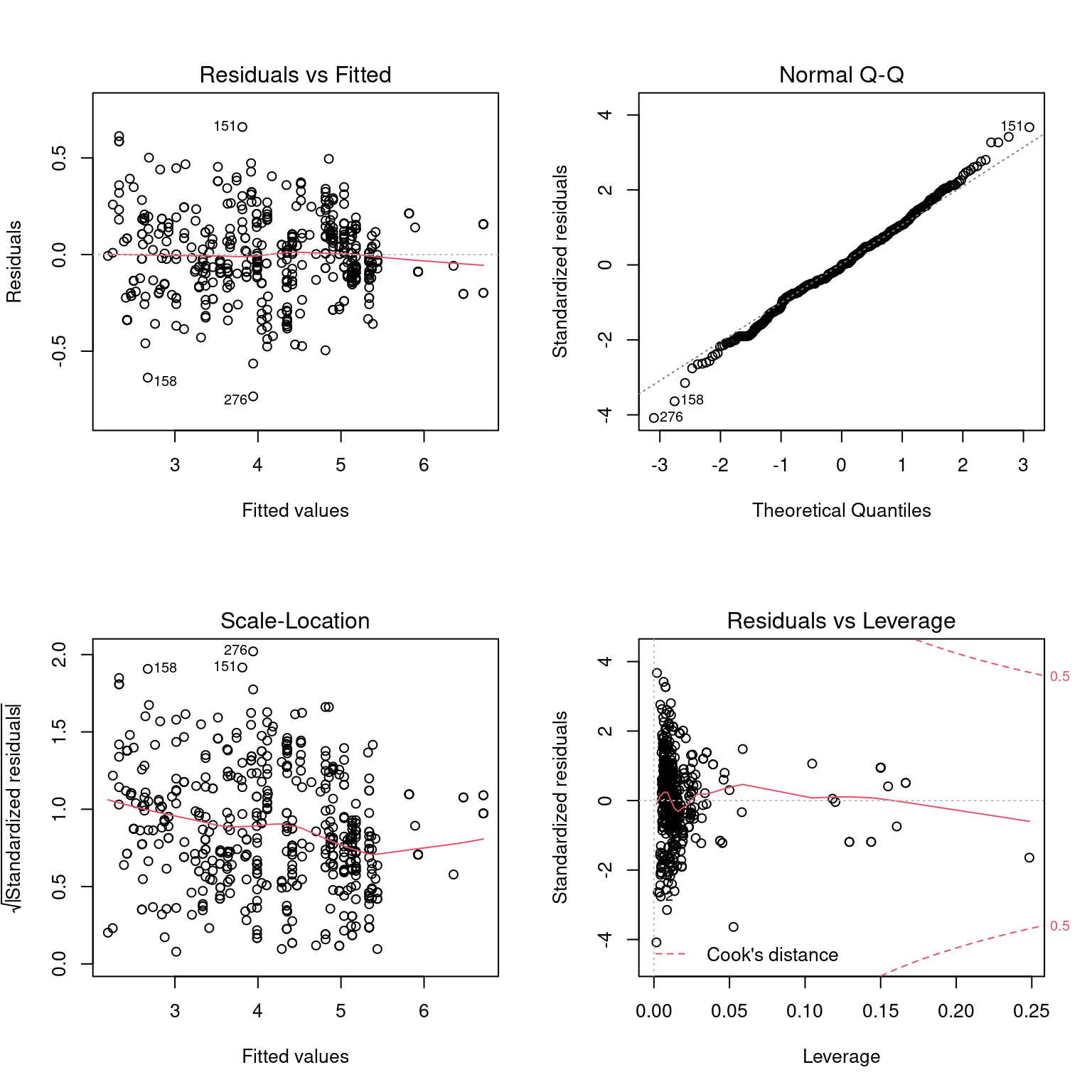
Figura 3.6: Análise de diagnóstico do segundo modelo ajustado. Resíduos versus valores ajustado (superior esquerda), raíz quadrada do valor absoluto dos resíduos padronizados (inferior esquerda), gráfico quantil-quantil dos resíduos (superior direita) e resíduos padronizados versus alavancagem (inferior direita).
3.3 Discussão
Nessa seção fizemos a análise descritiva e quantitativa dos dados coletados. Logo na análise descritiva identificamos que a variável reposta estava em uma escala não adequada e aplicamos uma transformação Box-Cox que facilitou a construção posterior do modelo. Também constatamos que as covariáveis escolhidas para a análise eram correlacionadas ao preço, indicando que poderiam fornecer um bom ajuste. Isso se constatou logo no primeiro ajuste do modelo, realizado no Código 3.1, porém ainda havia problemas nos resíduos que precisam ser corrigidos. O segundo ajuste, presente no Código 3.2, fez as correções necessárias. O modelo final forneceu uma boa explicação da variabilidade do preço, com \(R^2\) = 0.956. Embora as covariáveis fossem correlacionadas entre si, não houve problema de multiconearidade. Os resultados mostram que nossa é razoável hipótese de que o ano de lançamento, o número de núcleos e a frequência do processador explicam a variação do preço médio.
A Figura 3.7 mostra os valores preditos versus os valores observados do modelo ajustado no Código 3.2. Nota-se que o modelo de adequou bem aos dados, especialmente para os processadores de menor valor. Também, fica evidente a importância da segunda amostragem, uma vez que quase todos os valores maiores que 3,000 R$ foram obtidos através dela.
Cabe ressaltar que não observamos todo o domínio da covariável nucleos e foi ajustado um polinômio de segundo grau para ela, por isso, esse modelo não é recomendado para a predição de preço para processadores com mais de 32 núcleos.
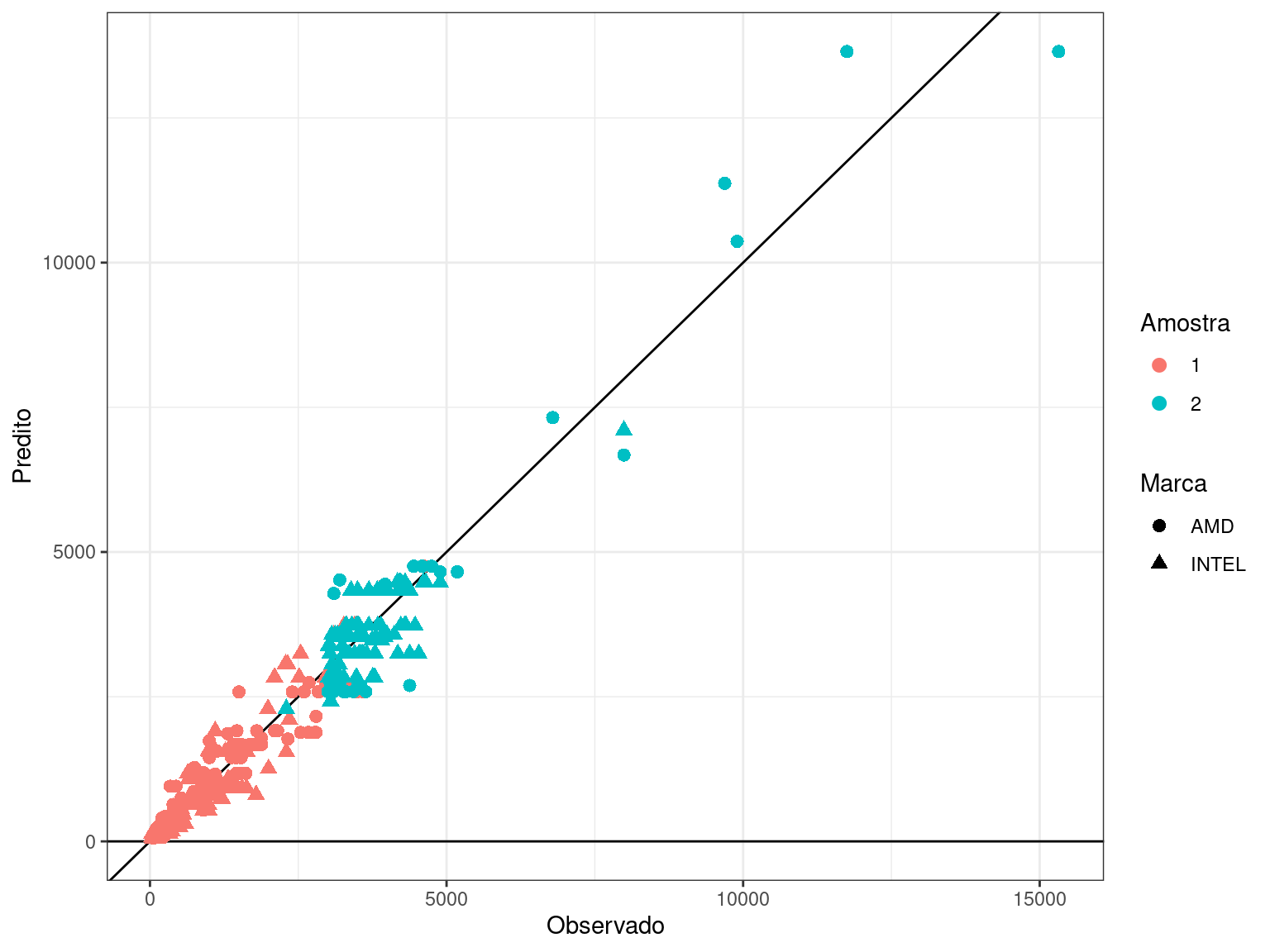
Figura 3.7: Valores preditos versus valores observados, para o segundo modelo ajustado.